Improved Inapproximability for TSP
Theory of Computing, Volume 10(9), pp. 217-236, 2014
Bibliography with links to cited articles
[1] Piotr Berman and Marek Karpinski: On some tighter inapproximability results (extended abstract). In Proc. 26th Internat. Colloq. on Automata, Languages and Programming (ICALP’99), volume 1644 of LNCS, pp. 200–209. Springer, 1999. [doi:10.1007/3-540-48523-6_17]
[2] Piotr Berman and Marek Karpinski: Efficient amplifiers and bounded degree optimization. Electron. Colloq. on Comput. Complexity (ECCC), 8(53), 2001. ECCC.
[3] Piotr Berman and Marek Karpinski: Improved approximation lower bounds on small occurrence optimization. Electron. Colloq. on Comput. Complexity (ECCC), 10(8), 2003. ECCC.
[4] Hans-Joachim Böckenhauer, Juraj Hromkovič, Ralf Klasing, Sebastian Seibert, and Walter Unger: An improved lower bound on the approximability of metric TSP and approximation algorithms for the TSP with sharpened triangle inequality. In Proc. 17th Ann. Symp. on Theoretical Aspects of Comp. Sci. (STACS’00), volume 1770 of LNCS, pp. 382–394. Springer, 2000. [doi:10.1007/3-540-46541-3_32]
[5] Nicos Christofides: Worst-case analysis of a new heuristic for the travelling salesman problem. Technical report, Carnegie-Mellon University, 1976.
[6] Lars Engebretsen: An explicit lower bound for TSP with distances one and two. Algorithmica, 35(4):301–319, 2003. Preliminary version in STACS’99. [doi:10.1007/s00453-002-1001-6]
[7] Lars Engebretsen and Marek Karpinski: TSP with bounded metrics. J. Comput. System Sci., 72(4):509–546, 2006. Preliminary version in ICALP’01. [doi:10.1016/j.jcss.2005.12.001]
[8] Shayan Oveis Gharan, Amin Saberi, and Mohit Singh: A randomized rounding approach to the traveling salesman problem. In Proc. 52nd FOCS, pp. 550–559. IEEE Comp. Soc. Press, 2011. [doi:10.1109/FOCS.2011.80]
[9] Johan Håstad: Some optimal inapproximability results. J. ACM, 48(4):798–859, 2001. Preliminary version in STOC’97. [doi:10.1145/502090.502098]
[10] Marek Karpinski, Michael Lampis, and Richard Schmied: New inapproximability bounds for TSP. In Proc. 24th Internat. Symp. on Symbolic and Algebraic Computation (ISAAC’13), volume 8283 of LNCS, pp. 568–578. Springer, 2013. See also at ECCC. [doi:10.1007/978-3-642-45030-3_53]
[11] Marek Karpinski and Richard Schmied: On approximation lower bounds for TSP with bounded metrics. Electron. Colloq. on Comput. Complexity (ECCC), 19(8), 2012. ECCC. See also at arXiv.
[12] Michael Lampis: Improved inapproximability for TSP. In Proc. 15th Internat. Workshop on Approximation Algorithms for Combinatorial Optimization Problems (APPROX’12), volume 1770 of LNCS, pp. 243–253. Springer, 2012. See also at arXiv. [doi:10.1007/978-3-642-32512-0_21]
[13] Tobias Mömke and Ola Svensson: Approximating graphic TSP by matchings. Technical report, 2011. Preliminary version in FOCS’11. [arXiv:1104.3090]
[14]
Marcin Mucha: 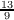 -approximation for graphic TSP. Theory Comput. Syst.,
2012. Preliminary version in STACS’12. [doi:10.1007/s00224-012-9439-7]
-approximation for graphic TSP. Theory Comput. Syst.,
2012. Preliminary version in STACS’12. [doi:10.1007/s00224-012-9439-7]
[15] Christos H. Papadimitriou and Santosh Vempala: On the approximability of the traveling salesman problem (extended abstract). In Proc. 32nd STOC, pp. 126–133. ACM Press, 2000. [doi:10.1145/335305.335320]
[16] Christos H. Papadimitriou and Santosh Vempala: On the approximability of the traveling salesman problem. Combinatorica, 26(1):101–120, 2006. Preliminary version in STOC’00. [doi:10.1007/s00493-006-0008-z]
[17] Christos H. Papadimitriou and Mihalis Yannakakis: The traveling salesman problem with distances one and two. Math. Oper. Res., 18(1):1–11, 1993. [doi:10.1287/moor.18.1.1]
[18] András Seb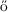 and Jens Vygen: Shorter tours by nicer ears:
7/5-approximation for graphic TSP, 3/2 for the path version, and 4/3
for two-edge-connected subgraphs. Technical report, 2012. To appear in
Combinatorica. [arXiv:1201.1870]
and Jens Vygen: Shorter tours by nicer ears:
7/5-approximation for graphic TSP, 3/2 for the path version, and 4/3
for two-edge-connected subgraphs. Technical report, 2012. To appear in
Combinatorica. [arXiv:1201.1870]
